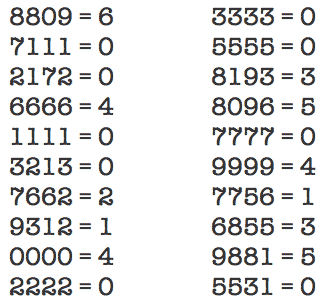
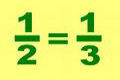 | Dê uma olhada nas relações de igualdade abaixo e tente descobrir qual é a fórmula secreta que é utilizada para obter cada resultado a partir dos números iniciais. Aham... não contavam com esta né? Pode fundir a cuca meu chapa! |
Importante: esperem pelo menos 24 horas antes de publicar a solução nos comentários, para que todo mundo possa tentar encontrar. Quem não quiser receber nenhuma ajuda nem pista para encontrar a solução do problema proposto talvez prefira não ler os comentários.
O MDig precisa de sua ajuda.
Por favor, apóie o MDig com o valor que você puder e isso leva apenas um minuto. Obrigado!
Meios de fazer a sua contribuição:
- Faça um doação pelo Paypal clicando no seguinte link: Apoiar o MDig.
- Seja nosso patrão no Patreon clicando no seguinte link: Patreon do MDig.
- Pix MDig: 461.396.566-72 ou luisaocs@gmail.com
- Depósito direto em conta corrente do Banco do Brasil: Agência: 3543-2 / Conta corrente: 17364-9
- Depósito direto em conta corrente da Caixa Econômica: Agência: 1637 / Conta corrente: 000835148057-4 / Operação: 1288



Faça o seu comentário
Comentários
« Ant. | Primeira | 1 | 2 | | Última | Prox. »
isto ai no e formula de jogo do bicho e nadax
Boa noite reeh cara como e isso de circulo pra ganhar nu jogo do bicho mim passar aí ok eu agradeço muito
olha eu esperava resultados para formar uns números pra ganhar kkkkkkkkk,mais valeu sai com a cuca fundida abraços.
tá entendi alguma coisa mas a pergunta é como uso isso no resultado do bicho?
numeros primos e nao primo.
??
Com resposta fica facinho, se ferro Admin.
1,2,3,5,7 = 0
0, 9 = 1
8 = 2
o 9999 da todos os resultados do jogo do bicho
É isso aí. o que vale é o nr de bolinhas:Ex:
0 é 1 bolinha
6 tem 1 bolinha em baixo
8 tem 2 bolinhas 1 em cima e outra em baixo
9 tem 1 bolinha em cima
Os nrs 1, 2 , 3, 4, 5 e 7 não são formados por bolinhas.
Volte ao problema e resolva somando as bolinhas
hahahaha não é questão de cálculo e sim lógica...
é só contar o círculos. Ex:
0 = 1
2 = 0
3 = 0
4 = #
5 = 0
6 = 1
7 = 0
8 = 2
9 = 1...
Logo,
2581 = 2 ^^
Ops...
Vício do Ctrl+C ctrl+V
Muito Simples...
se 0000=4, então, 0=1
se 1111=0, então, 1=0
se 2222=0, então, 2=0
se 3333=0, então, 3=0
se 5555=0, então, 5=0
se 6666=4, então, 6=1
se 7777=0, então, 7=0
se 9999=4, então, 9=1
Se, 8809=6, mas 0=1, e 9=1, então, 8=2
Basta .. Feito...
é só substituir e comprovar...
Números primos não funciona... não mesmo...
Muito Simples...
se 0000=4, então, 0=1
se 1111=0, então, 0=0
se 2222=0, então, 0=0
se 3333=0, então, 0=0
se 5555=0, então, 0=0
se 6666=4, então, 0=1
se 7777=0, então, 0=0
se 9999=4, então, 0=1
Se, 8809=6, mas 0=1, e 9=1, então, 8=2
Basta .. Feito...
é só substituir e comprovar...
Números primos não funciona... não mesmo...
A formula não opera os numeros, conforme o enunciado.
A resposta é sequer possive de ser escrita em uma formula matematica. Não perca seu tempo
pelo amor de deus...qual he a soluçaooo???
na verdade gastei somente meia hora
O que que esse tal moonwalker escreveu ?
eu não achei o post dele pra eu ler
aff
o luiz felipe precisou de mais de dias para resolver e tirar onda com algo que pramim eh inutil
ja o moonwalker percebeu a forma dos numeros e criou um teorema a partir disso
enquanto luiz felipe LOtou os comentarios de numeros que quase ninguem entende
moonwalker provou com um teorema qua bate certinho com a formula do problema
como ele disse "a vida eh bem melhor com simplicidade"
ou foi quase isso q ele disse Hehe
O moon deve tá certo :clap:
Meu voto vai pra teoria das bolinhas nos números ,hehhe
(mas faz sentido do que a dos números primos )
to com a anelise e nao abro uhsuhas
é...
o que conta são as circunferencias de cada número mesmo
boa análise Annelise
Compartilho e parabenizo ao Annelise pela sua observação.
naum entendi nada
eu fico com o comentário da annelise, eu testei e vi q tm td a vê.
ah va va va! procure nos hexadecimais! lá esta a resposta! ;D
Num saquei ;P
Os amigos da álgebra "boleana" tem todo o meu apoio.
Em cada um dos números com 4 dígitos, o resultado se refere ao número de circunferências que formam os algarismos. Pode até haver outra resposta, porém essa é uma coincidência que não pude deixar de perceber. Exemplo: 4568 = 3 pois o número 6 é formado (em parte) por uma circunterência e o número 8, por duas circunferências, logo o resultado será 3. Confira!
Moonwalker já disse tudo
Essa salada de frutas não abre meu apetite não. Minha praia não é as exatas.
eu intendi foi tu que não entendeu
se um não é primo então 1111=4(como tu falo)
mas no problema 1111=0
tu tem uma teoria mas testando-a poucas veses fica facil de diser que ela é perfeita :wink:
(procure no wikipedia, ou se mate e pergunte ao euclides)
UM NAO EH PRIMO, quantas vezes vou precisar dizer isso
o paulo acertou por pouco
o certo é quantidade de algarismos não primos somada a quantidade de oitos ( 8 ) e de ums (1)
- o resultado é quantas bolinhas tem no número. Exemplo: 8 tem duas bolinhas, zero tem 1 bolinha. etc.
huahuahuahua!!!!
:fool: :fool: :fool:
Fundiu minha cuca... :fool:
Fico com a teoria do Moon... :wink:
Raposinha esperta hein...
Por isso sou sua fã. :wink:
o paulo e o luis erraram
prova
como esta no problema:
1111=0
de acordo com a logica deles:
1111=4
8)
eu tenho muitas dúvidas.. mas em suma é pq da vida nada sei mesmo!!
Toda pessoa extremamente inteligente é cheia de dúvidas. Eu acho.
porque nao da para copiar e colar do excel e ficar certinho os tabs, que coisa em
Usem isto que vão responder qualquer sentença matemática: (X²+2X*Y+Y²), produtos notávéis, ensinam na 7ª série e vc utiliza pelo resto da vida. Traduzindo:
O quadrado do primeiro mais duas vezes o primeiro vezes o segundo mais o segundo ao quadrado.
quantidade de algarismos não primos somada a quantidade de oitos que aparece no número, voce quase conseguiu, mas presta atencao, foi por pouco. a matematica resolve sim.
quantidade de algarismos não primos somada a quantidade de oitos (8) e de ums (1)
detalhe: 1 não é primo (pergunte para o Euclides)
algarismos primos = 2, 3, 5, 7
algarismos nao primos = 0, 1, 4, 6, 8, 9
original não primos mais 8 total com 1 total diferenca
8809 = 6 8809 = 4 88xx = 2 6 xxxx = 0 6 0
7111 = 0 x111 = 3 xxxx = 0 3 x111 = 3 0 0
2172 = 0 x1xx = 1 xxxx = 0 1 x1xx = 1 0 0
6666 = 4 6666 = 4 xxxx = 0 4 xxxx = 0 4 0
1111 = 0 1111 = 4 xxxx = 0 4 1111 = 4 0 0
3213 = 0 xx1x = 1 xxxx = 0 1 xx1x = 1 0 0
7662 = 2 x66x = 2 xxxx = 0 2 xxxx = 0 2 0
9312 = 1 9x1x = 2 xxxx = 0 2 xx1x = 1 1 0
0000 = 4 0000 = 4 xxxx = 0 4 xxxx = 0 4 0
2222 = 0 xxxx = 0 xxxx = 0 0 xxxx = 0 0 0
3333 = 0 xxxx = 0 xxxx = 0 0 xxxx = 0 0 0
5555 = 0 xxxx = 0 xxxx = 0 0 xxxx = 0 0 0
8193 = 3 819x = 3 8xxx = 1 4 x1xx = 1 3 0
8096 = 5 8096 = 4 8xxx = 1 5 xxxx = 0 5 0
7777 = 0 xxxx = 0 xxxx = 0 0 xxxx = 0 0 0
9999 = 4 9999 = 4 xxxx = 0 4 xxxx = 0 4 0
7756 = 1 xxx6 = 1 xxxx = 0 1 xxxx = 0 1 0
6855 = 3 68xx = 2 x8xx = 1 3 xxxx = 0 3 0
9881 = 5 9881 = 4 x88x = 2 6 xxx1 = 1 5 0
5531 = 0 xxx1 = 1 xxxx = 0 1 xxx1 = 1 0 0
de qualquer maneira o moonwalker resolveu sem matematica
mas a minha formula booleana resolveu o problema com uma formula somente. e sem a algebra booleana nao funcionariam os pcs. apesar da aparente complexidade (so porque voce nao entende algebra booleana) nao esta incorreto, pois nao existe restricao que deveria usar somente algebra elementar.
mas como foram apresentadas 3 formas de resolver o problema, podem existir mais hhehe
Fácil, é a quantidade de algarismos não primos somada a quantidade de oitos que aparece no número.
teh a próxima pessoal! o/
acho que o Moonwalker tem razão, afinal tem que ser apenas UMA fórmula para todos os números e não várias fórmulas como estão postando, mas sei lá, ADMIN, salve-nos.... huaheuhauehu
Pois é... o andarilho lunar acertou essa, eu já tinha feito um parecido só q o outro levava em conta os ângulos do desenho do número :/
a raposa tah certa
ops, comi o 3
ai vai correto
x = { ~(x = 1111 ^ x = 2172 ^ x = 2222 ^ x = 3213 ^ x = 3333 ^ x = 5531 ^ x = 7111 ^ x = 7777) --> 0, ~( x = 7756 ^ x = 9312 ) --> 1, x = 7662 --> 2, ~( x = 6855 ^ x = 8193 ) --> 3, ~( x = 0 ^ x = 6666 ^ x = 9999 ) --> 4, ~( x = 8096 ^ x = 9881 ) --> 5, x = 8809 --> 6 }
satisfeito?
note que nao teve restricao da algebra neh, nem de qual ferramenta matematica usar para resolver o problema
agora sim, esse é o certo, posso tentar uma terceira vez nao posso hehehehe:
usando uma formula somente:
(ninguem disse qual algebra era para usar, estou usando a booleana hehe, ainda é matematica)
x = { ~(x = 1111 ^ x = 2172 ^ x = 2222 ^ x = 3213 ^ x = 3333 ^ x = 5531 ^ x = 7111 ^ x = 7777) --> 0, ~( x = 7756 ^ x = 9312 ) --> 1, x = 7662 --> 2, ~( x = 6855 ^
x = 8193 ), ~( x = 0 ^ x = 6666 ^ x = 9999 ) --> 4, ~( x = 8096 ^ x = 9881 ) --> 5, x = 8809 --> 6 }
leia o enunciadoe vera que a restrição de uma conta pra todas as igualdades
''ente descobrir qual é a fórmula secreta que é utilizada para obter cada resultado a partir dos números iniciais''
qual é A formula e não AS formulas
talvez eu tenha errado no maldito portugues, mas posso explicar as formulas matematicas, pelo menos as formulas estao certas, fui eficiente mas nao eficas ehehe. fiz certo mas nao o que foi pedido. tambem nao prestei atencao, estava estressado, fiz so para relaxar.
8096 = 6 =====> 8 - ( 8 ^ 0 ) - 9 = 6
7111 = 0 =====> 7 + 1 * ( 1 - 1 ) = 0
2142 = 0 =====> 2 ^ ( 1 ^ 7 ) - 2 = 0
6666 = 4 =====> log6 ( 6 * 6 * 6 * 6 ) = 4
1111 = 0 =====> 1 * 1 * ( 1 - 1 ) = 0
3213 = 0 =====> ( 3 - 2 - 1 ) * 3 = 0
7662 = 2 =====> 7 * ( 6 - 6 ) + 2 = 2
9312 = 1 =====> ( 9 / 3 / 1 ) - 2 = 1
0000 = 4 =====> antilog ( 0 ) + antilog ( 0 ) + antilog ( 0 ) + antilog ( 0 ) = 4
2222 = 0 =====> ( 2 - 2 ) * 2 * 2 = 0
3333 = 0 =====> 3 + 3 * ( 3 - 3 ) = 0
5555 = 0 =====> 5 + 5 * ( 5 - 5 ) = 0
8193 = 3 =====> 8 + 1 - 9 + 3 = 3
8096 = 5 =====> 8 - 0 - 9 + 6 = 5
7777 = 0 =====> 7 + 7 * ( 7 - 7 ) = 0
9999 = 4 =====> log9 ( 9 * 9 * 9 * 9 ) = 4
7756 = 1 =====> 7 - 7 - 5 + 6 = 1
6855 = 3 =====> - 6 + 8 + ( 5 / 5 ) = 3
9881 = 5 =====> 9 - log4 ( 8 * 8 ) - 1 = 5
5531 = 0 =====> ( 5 - 5 ) * 3 * 1 = 0
para quem nao lembra
log x ( y ) = z =====> x ^ z = y
y = antilog ( x ) =====> y = e ^ x
x ^ 0 = 1
« Ant. | Primeira | 1 | 2 | | Última | Prox. »