 | Imagina que você está em uma festa, rodeado de uma ou duas dúzias de amigos. Qual é a probabilidade de que um par deles faça aniversário no mesmo dia? Ainda que pareça incrível, é possível demonstrar matematicamente que se o número de convidados for de 23 pessoas, a probabilidade supera os 50%. E se houver mais de 60 convidados, pode apostar que dois deles aniversariam no mesmo dia com 99% de possibilidades de acerto. |
O Paradoxo do aniversário estabelece que se existem 23 pessoas em uma reunião, a probabilidade de que ao menos duas delas aniversariam no mesmo dia é de 50,7%. A percentagem parece meio alta pois poderíamos raciocinar que 23/365*100 = 6,3%. Crasso erro! Na realidade estamos calculando qual é a probabilidade de que algum dos presentes aniversarie em um dia em particular, algo que nada tem a ver com o problema. Para calcular realmente a probabilidade de que duas pessoas do grupo façam aniversário no mesmo dia, é necessário considerar os pares e não só uma pessoa. Vejamos como é a forma correta de fazer isto.
Suponhamos então que em nossa festa se encontram as 23 pessoas que podem formar 23 x 22 = 253 pares diferentes entre elas. Começamos calculando primeiro a probabilidade de que "n" aniversários sejam diferentes. Esta probabilidade é dada pela seguinte equação:
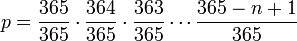
O que representam essa série de frações é o fato de que a segunda pessoa não pode ter o mesmo aniversário que o primeiro (364/365), a terceira pessoa não pode ter o mesmo aniversário que as duas primeiras (363/365), e assim sucessivamente. Podemos simplificar muito essa fórmula se utilizamos os chamados números fatoriais que se aplicados na equação anterior permitem escrever uma nova equação da seguinte maneira:
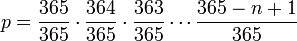
Na qual "p" é a probabilidade de que duas pessoas não façam aniversário no mesmo dia. Para encontrar o resultado que estamos buscando -a probabilidade que ao menos duas pessoas aniversariem na mesma data- devemos fazer 1-p. Se achar que a equação é muito complicada para ser revolvida, adianto o resultado. Para n = 23 obtém-se um valor de 0,507, uma probabilidade ao redor de 50,7%.
Da próxima vez que estiver em uma uma festa na qual tenham outros 20 ou 30 convidados, verifique se dois deles aniversariam no mesmo dia. Se forem mais de 50, você pode até pegar o microfone e fazer uma aposta com uma grande probabilidade de ganhar e voltar para casa com a garota mais bonita da festa. E se perder, pode passar o tempo calculando as remotas possibilidades de que uma catástrofe assim ocorresse.
O MDig precisa de sua ajuda.
Não conseguirmos fazer frente aos custos este mês porque o AdSense zerou. Cada contribuição, seja grande ou pequena, faz uma diferença real para o nosso futuro. Por favor, apóie o MDig com o valor que você puder e isso leva apenas um minuto. Obrigado!
Meios de fazer a sua contribuição:
- Faça um doação pelo Paypal clicando no seguinte link: Apoiar o MDig.
- Seja nosso patrão no Patreon clicando no seguinte link: Patreon do MDig.
- Pix MDig ID: c048e5ac-0172-45ed-b26a-910f9f4b1d0a
- Depósito direto em conta corrente do Banco do Brasil: Agência: 3543-2 / Conta corrente: 17364-9
- Depósito direto em conta corrente da Caixa Econômica: Agência: 1637 / Conta corrente: 000835148057-4 / Operação: 1288
Faça o seu comentário
Comentários
No quarteirão da minha rua, existem mais três pessoas que fazem aniversário junto comigo. Neste mesmo dia (04/02) é niver da minha cidade. Isto eu considero um fato raro.
heh, minha mãe e meu pai fazem aniversário no mesmo dia. (:
ah tah... é igual o brasileirão..todos x todos...entendi... então 30 x 29 = 870....quase três chances de acertar. ah esquece
@Duddz
LOL
Se você tem 700+ pessoas no seu orkut, É ÓBVIO que alguém vai fazer aniversário no mesmo dia. u.u'
Cada um, viu.
Quando eu estudava no ensino médio, o meu colégio tinha o costume de mandar cartões de "feliz aniversário" para os aniversariantes do dia.
Cada classe tinha no mínimo 45 alunos, eram 5 classes.
45 x 5 = 225 alunos no mínimo.
Tirando os alunos que faziam aniversário entre dezembro e fevereiro, só um ou dois pares de pessoas recebiam o cartão no mesmo dia.
Talvez o fato de ter três meses a menos, fure o calculo.
Éssa é legal, vi no primeiro o segundo perioda da facul.
Caso não encontre uma pessoa dentre os integrantes do grupo, é só extender para os pais das pessoas na sala que é quase certo que faça aniversário no mesmo dia que você, em sem tratando que aumentou o espaço amostral duas vezes mais.
Dr. Muceta, posso afirmar com praticamente 100% de certeza que o senhor está enganado. Calculei a probabilidade na HP e ela não tem precisão o bastante pra me dar o quanto o resultado é menor do que 100% (visto que essa diferença é extremamente pequena).
O que deve ter acontecido é que vc não reparou a vez em que duas pessoas aniversariaram juntas...
eu faço hoje Ô/
quase nunca acho ninguém que faz no mesmo dia que eu
DR muceta, no meu orkut tenho 700 pessoas e quase todo dia tem uma, duas ou 3 pessoas fazendo aniversario
Acho isso uma errada...no meu orkut possuo 251 amigos e nunca apareceram dois aniversariantes no mesmo dia.
Hehehehehe
Princípio das gavetas de Dirichlet, também conhecido como principio da casa dos pombos... esse foi o tema da minha monografia do bacharelado em Matemática... hehehehehe... muito boa essa aplicação... mas tem outras muito interessantes também!!!! é análise combinatória!!!!
Eu faço dia 07/12...
Alguém mais?!!
Entendi tudo
Corvino... vc é de uma logica e de um discernimento que permita-me elogiá-lo... Realmente, festa de aniversário é um saco. Tem até um leve cheiro de naftalina. O grande lance é tomar os goró e tentar garfar uma franga... (desde que a dona do barraco não tenha ido...)
meu pai e a lee redmond(mulher com as maiores unhas do mundo) fazem aniversario 2 de fevereiro.
nao entendi muito naum, mas achei interessante
não intindi....
morri, n acompanhei nada que você falou =)
Opa! Gostei disso! Na próxima festa com casa cheia que eu for, vou propor isso e se eu ganhar cada um me dá dez contos
maneiro... festa de aniversário coletiva! êêê
Pô, eu enxerguei esse problema por outro ângulo...
São 253 pares de pessoas.
Qual a probabilidade de que um desses pares tenham duas pessoas fazendo aniversário no mesmo dia? 1/365,25 (considerando os anos bissextos)
Esse evento deve ser checado 253 vezes (pois são 253 pares).
Logo, são 253 ocorrências vezes 1/365.25 de probabilidade, ou seja 0,69, ou 69%.
Tá certo isso?
Abs!
Concordo contigo, Corvino
msp1500
na verdade a explicação disso é proque você não especificou em qual das datas de aniversario avera a coincidencia(quando estudei probabilidade tambem não acreditei, é tosco, mas no fim você descobre que podia ter feito algo melhor que observar esse fato
se não me engano se forem 35 pesssoas a chance é de 95%
Você terá 50% de chance de bancar o bobo na frente de todo mundo. E a garota mais bonita da festa não vai embora com o nerd. Esqueça isso e curta a festa.
Ou não...
Acho que isso é balela. especulação. Não acredito nisso não, pois a probabilidade de cada um deles fazer aniversário em dias diferentes também existe, e é muito mais fácil de acontecer.
Que preguiça de ler mas tem uma pessoa aqui onde estou que bem quando estava lendo disse que fazia aniversario no mesmo dia q eu
PRIMEIRÃO. Pelo menos um, né?